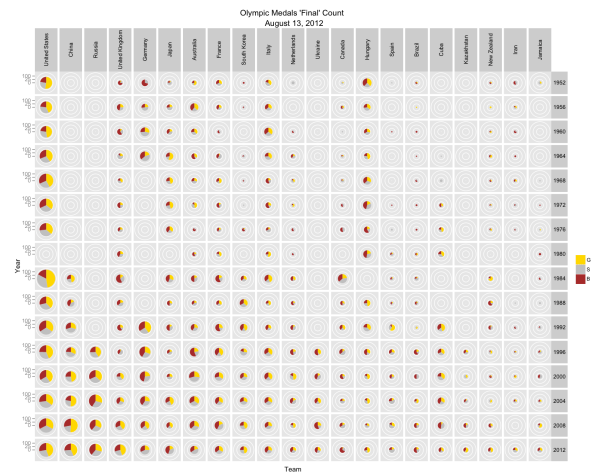
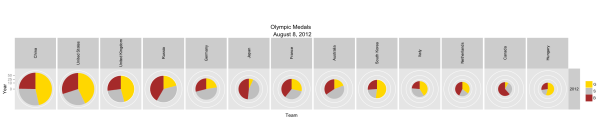
Category Archives: Sports
Mere Mortals: Some Interesting Tweets
On Monday, I posted in response to Bill Barnwell’s article on Grantland called “Mere Mortals” where he makes the claim that regular NFL players who played between 1959 and 1988 have a statistically significantly lower mortality rate than regular baseball players of the same era. I suspect all that has been demonstrated is that older people die more often than younger people because the groups are not directly comparable, since age was not controlled for in the comparison. What I believe we are dealing with here is correlation and not causation. Baseball, almost surely, is not killing people faster than baseball players. And even if it was, it has not been demonstrated. Not even close.
So, I’ve been reading some other stuff by Barnwell (which I really enjoy) including his Twitter feed lately and two particular tweets interested me greatly. The first one:
Appreciate the kind words about the study. For those who asked: Average age of MLB player at time of passing was 60.9; for NFL, it was 58.8.
And the second one:
Went back and looked at age for all players in my study by request; MLB players in sample were on average 24 months older than NFL players.
The first tweet should make someone pause and think about how this can be, while at the same time, baseball players have a higher mortality rate. I suspected, originally, and still do, that it was because one group was simply older than the other group. Which…..is exactly what was tweeted in the second tweet. MLB players in the sample were TWO YEARS older than NFL players in the sample. Can you name something that 62 year olds do more often than 60 year olds? I can. They die more often.
So, it seems to me like all that the study has actually demonstrated is that older people die more often. So, maybe Barnwell will dial back his “stunning” claims? Maybe not. This is the tweet directly before tweet number 2:
ICYMI: Wrote about the stunning respective mortality rates of MLB and NFL players from 1959-88 on
@grantland33. http://ow.ly/d1QGH
Cheers.
MLB rankings – 8/20/2012
StatsInTheWild MLB rankings as of August 20, 2012 at 12:18pm. SOS=strength of schedule
| Team | Rank | Change | Record | ESPN | TeamRankings.com | SOS | Run Diff |
| NYY | 1 | – | 75-50 | 4 | 1 | 4 | +102 |
| Texas | 2 | – | 71-50 | 5 | 3 | 13 | +89 |
| Tampa Bay | 3 | ↑6 | 68-54 | 7 | 4 | 5 | +69 |
| Washington | 4 | – | 76-46 | 1 | 2 | 23 | +109 |
| Oakland | 5 | – | 65-56 | 13 | 6 | 8 | +32 |
| Atlanta | 6 | ↑4 | 70-52 | 3 | 5 | 21 | +84 |
| Chi WSox | 7 | ↓2 | 66-55 | 9 | 10 | 14 | +67 |
| Cincinnati | 8 | ↓2 | 74-49 | 2 | 7 | 30 | +73 |
| Detroit | 9 | ↓1 | 64-57 | 12 | 9 | 12 | +24 |
| LA Angels | 10 | ↓7 | 62-60 | 15 | 11 | 7 | +21 |
| Boston | 11 | – | 59-63 | 17 | 12 | 3 | +34 |
| Baltimore | 12 | ↑2 | 66-56 | 14 | 8 | 2 | -47 |
| St. Louis | 13 | – | 65-56 | 11 | 17 | 29 | +106 |
| Toronto | 14 | ↓2 | 56-65 | 19 | 18 | 1 | -25 |
| Seattle | 15 | ↑1 |
59-64 | 20 | 13 | 6 | 0 |
| LA Dodgers | 16 | ↑3 | 67-56 | 10 | 16 | 25 | +38 |
| Arizona | 17 | – | 62-60 | 16 | 19 | 24 | +40 |
| SF | 18 | – | 67-55 | 8 | 14 | 26 | +30 |
| Pittsburgh | 19 | ↓4 | 67-55 | 6 | 15 | 28 | +19 |
| Kansas City | 20 | ↑2 | 54-67 | 25 | 20 | 11 | -47 |
| NY Mets | 21 | ↓1 | 57-65 | 18 | 21 | 15 | -33 |
| Philadelphia | 22 | ↑3 | 57-65 | 22 | 22 | 18 | -30 |
| Cleveland | 23 | – | 54-68 | 23 | 24 | 9 | -125 |
| Milwaukee | 24 | – | 55-66 | 24 | 27 | 27 | -11 |
| Minnesota | 25 | ↓4 | 51-70 | 26 | 23 | 10 | -86 |
| Miami | 26 | – | 56-67 | 21 | 25 | 16 | -84 |
| San Diego | 27 | ↑1 | 54-70 | 27 | 26 | 22 | -70 |
| Chi Cubs | 28 | ↓1 | 47-75 | 28 | 29 | 20 | -98 |
| Colorado | 29 | – | 47-73 | 29 | 28 | 19 | -112 |
| Houston | 30 | – | 39-83 | 30 | 30 | 17 | -169 |
Past Rankings:
Cheers.
Grantland Newsflash: The old die more often than the young
Grantland recently published this article, Mere Mortals, which claims that:
Baseball players who accrued at least five qualifying seasons from 1959 through 1988 died at a higher rate than similarly experienced football players from the same time frame. The difference between the two is statistically significant6and allows us to reject the null hypothesis; there is a meaningful difference between the mortality rates of baseball players and football players with careers that emulated the [National Institute for Occupational Safety and Health] NIOSH criteria.
The authors then go on to collect data on football and baseball players who played at least 5 years between 1959 and 1988, and their results are below:
| Baseball | Football | |
|---|---|---|
| Qualifying Players | 1,494 | 3,088 |
| Alive | 1,256 | 2,694 |
| Deceased | 238 | 394 |
| Mortality Rate | 15.9 percent | 12.8 percent |
From this table, to their credit, they calculated confidence intervals for the mortality rate, as well as performing a fisher exact test to test for independence between the rows (dead or alive) and columns (baseball and football). For football players, the 95% confidence interval for the mortality rate was (11.6, 13.9), and, for baseball players, the 95% confidence interval was (14.1,17.8). The Fisher exact test gives a p-value of about 0.004 and from this they conclude, correctly, that the mortality rate is significantly different between the groups at the 0.01 level.
So, the big question is, as they pose it:
Why is it that baseball players from the ’60s, ’70s, and ’80s are dying more frequently than football players from the same era? Truthfully, as a layman, I can’t say with any certainty, and I don’t think it’s appropriate to speculate. A deeper study into the mortality rates of baseball players that emulated the NIOSH focus on specific causes of death versus the general population might prove valuable.
Well, I’ll “field” (pun intended) this one. Baseball players are dying more often because they are older that football players. The authors, as far as I can tell, never controlled for the age of the players, or any other risk factors for that matter. In 1959, there were, as far as I can tell, 12 NFL teams each with 40 players. That 480 players. In 1988, there were 28 teams with 59 players each; A total of 1652. In baseball, in 1959 there were 16 teams with, let’s use the largest number, 40 man teams, for a total of 640 players. That number in 1988 was 1040 (26 teams with 40 players). So there were almost 3 and half time more players in the NFL in 1988 than there were in 1959. The number of baseball players only increased about 1.6 times over this same period.
These numbers aren’t exact, but the point still stands: The group of football players that has been collected here has a greater proportion of younger people in it than the baseball group. So it’s not exactly apples to apples. In fact, it’s not even close. You’d expect, just based on the ages of the players in these groups for baseball players to have higher rates of mortality than the football players. So basically they have demonstrated that the old die more often than the young.
Cheers.
P.S. My first boss once gave me this example. Remember the ad where it was claimed that 90% of all trucks sold in the last ten years were still on the road? You’re comparing cars that are ten years old in the same group with cars that are less than a year old. Not exactly apples to apples.
Low hit, no hit, and perfect games: The King Felix Edition
Felix Hernandez of the Seattle Mariners just threw the third perfect game of the season, so I figured it was a good time to update my low hit games graphs that I posted in June. So, here they are:
MLB Rankings – 8/14/2012
StatsInTheWild MLB rankings as of August 6, 2012 at 8:17pm. SOS=strength of schedule
| Team | Rank | Change | Record | ESPN | TeamRankings.com | SOS | Run Diff |
| NYY | 1 | – | 63-44 | 3 | 1 | 5 | +92 |
| Texas | 2 | – | 63-44 | 4 | 2 | 13 | +83 |
| LA Angels | 3 | – | 58-51 | 9 | 6 | 7 | +49 |
| Washington | 4 | ↑2 | 65-43 | 2 | 4 | 23 | +82 |
| ChiSox | 5 | ↑4 | 59-48 | 7 | 5 | 14 | +64 |
| Cincinnati | 6 | ↑5 | 66-42 | 1 | 3 | 29 | +72 |
| Oakland | 7 | ↑1 | 58-50 | 8 | 7 | 8 | +28 |
| Detroit | 8 | ↓1 | 58-50 | 13 | 9 | 12 | +24 |
| TampaBay | 9 | ↑1 | 56-52 | 14 | 12 | 3 | +19 |
| Atlanta | 10 | ↑5 | 62-46 | 5 | 8 | 21 | +62 |
| Boston | 11 | ↓6 | 54-55 | 17 | 13 | 6 | +29 |
| Toronto | 12 | ↓8 | 53-55 | 18 | 14 | 2 | +9 |
| St. Louis | 13 | ↑1 | 59-49 | 10 | 15 | 30 | +110 |
| Baltimore | 14 | ↓2 | 57-51 | 16 | 11 | 1 | -57 |
| Pittsburgh | 15 | ↓2 |
61-46 | 6 | 10 | 28 | +36 |
| Seattle | 16 | ↑1 | 51-59 | 20 | 17 | 4 | -3 |
| Arizona | 17 | ↑4 | 55-53 | 15 | 19 | 26 | +42 |
| SF | 18 | ↓2 | 59-49 | 11 | 16 | 27 | +19 |
| LA Dodgers | 19 | ↓1 |
59-50 | 12 | 18 | 25 | +15 |
| NY Mets | 20 | – | 53-56 | 19 | 20 | 17 | -5 |
| Minnesota | 21 | ↑3 | 47-61 | 25 | 22 | 11 | -79 |
| Kansas City | 22 | – | 45-62 | 26 | 23 | 10 | -60 |
| Cleveland | 23 | ↓4 | 50-58 | 21 | 21 | 9 | -90 |
| Milwaukee | 24 | ↓1 | 48-59 | 22 | 26 | 19 | -13 |
| Philadelphia | 25 | – | 49-59 | 24 | 24 | 19 | -29 |
| Miami | 26 | – | 49-60 | 23 | 25 | 15 | -100 |
| Chic Cubs | 27 | ↑1 | 43-63 | 28 | 27 | 18 | -79 |
| San Diego | 28 | ↓1 | 46-64 | 27 | 28 | 22 | -61 |
| Colorado | 29 | – | 38-68 | 29 | 29 | 20 | -117 |
| Houston | 30 | – | 36-73 | 30 | 30 | 16 | -142 |
Past Rankings:
Cheers.
All-Star Plots?
Here are some star plots for major league baseball batters, pitchers, and ball parks. The star plots represent the outcomes of a particular at bat for a hitter, a pitcher, or at a given ball park. For each plot, batter, pitcher, and ball park was varied, while the other two parameters were filled in with the average value. For instance, all batters outcomes are calculated as if they were facing J. Kinney at Wrigley Field; Pitchers data was calculated as if they were facing K. Medlen at Wrigley; and Park factors were calculated as the outcome of J. Kinney vs K. Medlen at different ball parks. The data use to calculate these were downloaded from baseball-reference.com and includes the results every single plate appearance so far this season (about 125,000 so far) and where the game was played. Six outcomes to an at bat were considered: out, walk, single, double, triple, and home run. The probability of each of these events was estimated creating a vectors of probabilities with six elements corresponding to each of the six outcome considered. I’ve chosen to display this data using the star plots below. The key to the star plot can be found in the lower left corner of each plot and displays the probabilities of each outcome relative to other batters. For instance, a large blue pie piece on the left indicates that batter’s plate appearance ends with a HR more often relative to other players. Likewise, a large red pie on the right indicates that the batter’s plate appearance ends in an out more often than other players.
I’ve chosen 100 batters based on their wide range of hitting styles. In the first row, you’ll players who make outs at the lowest rates relative to other players. These include players like Joey Votto, Andrew McCutchen, David Wight, and Mike Trout. Further down, you’ll start to see players who you might describe as single’s hitters. These include players like Ruben Tejada, Derek jeter, B. Revere, and Juan Pierre. Finally, towards the bottom row, you’ll see the players who are primarily power hitters like Adam Dunn and Jose Bautista with large blue, for home run,s and orange, for walks, pie pieces, with significant red for outs. Other players on this row like Saltalamacchia, Plouffe, and Rosario have the large blue and significant red pieces, but they lack walks.
The star plot for pitchers is below. The first thing we need to say here is that Justin Verlander is very, very good at pitching a baseball. Some other interesting pitchers here are Yu Darvish, Edison Volquez, and Carlos Zambrano. They seem to give up relatively few hits, but they give up many more walks that the average pitcher.
These plots are ordered from highest to lowest probability that an out will be made in a given plate appearance. Pittsburgh, Seattle, and San Francisco lead the way in pitching friendly parks. These are the same as the bottom three according to ESPNs measure of Park factor. The most hitter friendly park is, no surprise, Coors field in Colorado. Other hitter friendly parks include Target and Chase field in Minnesota and Arizona, respectively. Arizona is expected here, but Minnesota is a little bit surprising. It looks like, while it is rare to make an out, most hits are only singles, which don’t generate as many runs are their extra base counterparts. Home run friendly parks include Coors, Chase, Camden Yards, Miller, Comisky, and Yankee Stadium. Fenway park is solidly in the hitter category, but it gets that way, rather than by giving up many homeruns, by yielding a greater percentage of doubles than any other park.
Cheers.
A novel way to gamble on the NCAA tournament…
I saw a talk at JSM where I was introduced to a fun new (well, new to me) game to play during the NCAA tournament. First, teams are assigned a price based on their seed. This can be done in many ways, but it was set in the talk that the one seeds cost 25 cents, the two seeds cost 19 cents, all the way down to the 15 and 16 seeds which were a penny each. The goal is to choose a set of teams, that costs, in total, one dollar, that will win the most number of games in the NCAA tournament. So picking all the number one seeds, which will cost exactly one dollar, but the most wins they can earn is 19 (4 each to the final four and then one each for the two semifinals and one for the championship). So, according to the speaker, this usually won’t get you the win. First of all, this game is awesome. Once you can stop thinking about how awesome this game is, the next logical question is: How do you choose the optimal set of teams?
Douglas Noe and his student Geng Chen used an evolutionary algorithm to optimize the selection of teams, and they used Ken Pomeroy’s rankings as a guide to the probability that one team will beat another team in the tournament. Now, I don’t think I ever heard of evolutionary algorithms, and, if I have, I’ve totally forgotten about them. But they are wicked cool. Here is the wikipedia page for evolutionary algorithms, and it’s worth checking out. Does anyone have any suggestions as to a good resource for an introduction to evolutionary algorithms?
Cheers.
MLB Rankings – 8/6/2012
StatsInTheWild MLB rankings as of August 6, 2012 at 8:17pm. SOS=strength of schedule
| Team | Rank | Change | Record | ESPN | TeamRankings.com | SOS | Run Diff |
| NYY | 1 | – | 63-44 | 3 | 1 | 5 | +92 |
| Texas | 2 | – | 63-44 | 4 | 2 | 13 | +83 |
| LA Angels | 3 | – | 58-51 | 9 | 6 | 7 | +49 |
| Washington | 4 | ↑2 | 65-43 | 2 | 4 | 23 | +82 |
| ChiSox | 5 | ↑4 | 59-48 | 7 | 5 | 14 | +64 |
| Cincinnati | 6 | ↑5 | 66-42 | 1 | 3 | 29 | +72 |
| Oakland | 7 | ↑1 | 58-50 | 8 | 7 | 8 | +28 |
| Detroit | 8 | ↓1 | 58-50 | 13 | 9 | 12 | +24 |
| TampaBay | 9 | ↑1 | 56-52 | 14 | 12 | 3 | +19 |
| Atlanta | 10 | ↑5 | 62-46 | 5 | 8 | 21 | +62 |
| Boston | 11 | ↓6 | 54-55 | 17 | 13 | 6 | +29 |
| Toronto | 12 | ↓8 | 53-55 | 18 | 14 | 2 | +9 |
| St. Louis | 13 | ↑1 | 59-49 | 10 | 15 | 30 | +110 |
| Baltimore | 14 | ↓2 | 57-51 | 16 | 11 | 1 | -57 |
| Pittsburgh | 15 | ↓2 |
61-46 | 6 | 10 | 28 | +36 |
| Seattle | 16 | ↑1 | 51-59 | 20 | 17 | 4 | -3 |
| Arizona | 17 | ↑4 | 55-53 | 15 | 19 | 26 | +42 |
| SF | 18 | ↓2 | 59-49 | 11 | 16 | 27 | +19 |
| LA Dodgers | 19 | ↓1 |
59-50 | 12 | 18 | 25 | +15 |
| NY Mets | 20 | – | 53-56 | 19 | 20 | 17 | -5 |
| Minnesota | 21 | ↑3 | 47-61 | 25 | 22 | 11 | -79 |
| Kansas City | 22 | – | 45-62 | 26 | 23 | 10 | -60 |
| Cleveland | 23 | ↓4 | 50-58 | 21 | 21 | 9 | -90 |
| Milwaukee | 24 | ↓1 | 48-59 | 22 | 26 | 19 | -13 |
| Philadelphia | 25 | – | 49-59 | 24 | 24 | 19 | -29 |
| Miami | 26 | – | 49-60 | 23 | 25 | 15 | -100 |
| Chic Cubs | 27 | ↑1 | 43-63 | 28 | 27 | 18 | -79 |
| San Diego | 28 | ↓1 | 46-64 | 27 | 28 | 22 | -61 |
| Colorado | 29 | – | 38-68 | 29 | 29 | 20 | -117 |
| Houston | 30 | – | 36-73 | 30 | 30 | 16 | -142 |
Past Rankings:
Cheers.